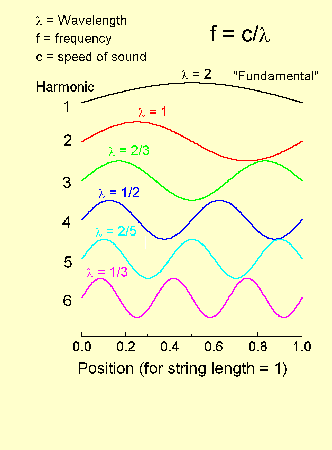
To understand how the scale arises from the overtone series, imagine vibrations on a string of fixed length, which is fixed at both ends (e.g. a piano string). The actual vibration may be very complicated, but can be broken down into basic units called "modes" of oscillation, each of which is a sine wave.
Since the string is fixed at both ends, so too must each of the
possible modes. Hence, only sine waves which do not oscillate at
the ends of the strings are allowed. The possibilities are
shown in the figure below.

The fixed ends of the string will allow only certain wavelength
modes to appear. If the wave speed is a constant
(a good approximation)
and, for the sake of an example, we take the frequency of the
fundamental mode to be that of C3 (the C below middle C, 131 Hz),
the overtones are harmonically related (they are integer
multiples of the fundamental) and are given in the following
table.
| Harmonic | Freq. Hz | Note | Comments |
|---|---|---|---|
| 1 | 131 | C3 | Fundamental |
| 2 | 262 | C4 | 1 Octave Higher |
| 3 | 393 | G4 | A Fifth above C4 |
| 4 | 524 | C5 | 2 Octaves above fund. and a fourth above G4 |
| 5 | 655 | E5 | A Third above C5 |
| 6 | 786 | G5 | A Fifth above C5 Harms. 4, 5 & 6 form a major chord |
| 7 | 917 | almost B5b | An overtone to avoid |
Since notes can be translated by an octave by multiplying or dividing the frequency by 2, these overtones of one fundamental define the notes C, E, and G. If we now make another string with a fundamental frequency corresponding to E3 (655/4 = 163.75 Hz) and look at its overtones, we define the notes B, and Ab. Starting with G3 (196.5 Hz), one gets an overtone defining D. Starting with D, the notes A and F# are overtones. Continuing the process, the notes of the scale are produced.
Questions/Comments to: suits@mtu.edu
There are no pop-ups or ads of any kind on these pages. If you are seeing them, they are being added by a third party without the consent of the author.
Back to Scales and Temperament.