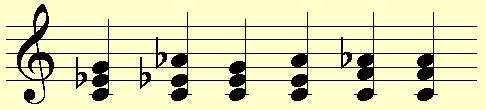
plus those where the notes are related by octaves. These are (in order) C-minor, Ab-major, C-major, A-minor, F-minor, and F-major chords.
| Chord | Half Steps between notes | Freq. Ratios |
|---|---|---|
| Major | 4-3 | 4:5:6 |
| Minor | 3-4 | 10:12:15 |
| Diminished | 3-3 | 160:192:231 (approx. 20:24:29) |
| 7th | 4-3-3 | 20:25:30:36 |
| Min. 7th | 3-4-3 | 10:12:15:18 |
| Maj. 7th | 4-3-4 | 8:10:12:15 |
The fundamental beat frequency associated with a chord can be determined by looking at the repeat period - that is, for the frequency ratios given above (which are reduced to the lowest possible integer values), the repeat period for the major chord is 4 times the period of the lowest note in the chord. For the 7th, it is 20 times that of the lowest note. Since f = 1/T, the fundamental beat frequency for the major chord is 1/4th the frequency of the lowest note, and for the 7th, it is 1/20th the frequency of the lowest note. If you listen carefully, you can hear the beat frequency as an additional unplayed note.
What makes a chord sound consonant or dissonant depends upon human physiology and psychology. One "rule" is based on work by Helmholtz and relies on "overlapping harmonics." A nice explanation is contained in the article by Jan Wild listed below. Basically, for each pair of notes in the chord, find the lowest harmonics which match. If it is the 8th or less in every case, the chord is consonant. For example, the major triad has frequency radios of 4:5:6. The harmonics of the lowest note are then 4, 8, 12, 16, 20, 24, etc. and the harmonics of the second are 5, 10, 15, 20, 25, etc. The fifth of the lower matches with the fourth of the upper so this interval should be consonant. (i.e. they are both less than the 9th harmonic). One gets a similar result for 4 and 6, and 5 and 6. Hence, the entire major triad is consonant.
If you try to use the rule of eight and the equal tempered scale, you will have to consider harmonics which "almost match" since none of them, except the octaves, will ever exactly match.
Based on this "rule of 8" the "nice" three note chords which start on middle C are:

plus those where the notes are related by octaves. These
are (in order) C-minor, Ab-major, C-major, A-minor, F-minor, and F-major
chords.
The rule of 8 is, of course, not an absolute rule but only serves as a guideline.
Chord progressions are the basis of most western music. If
a tune stays in one key, then the basic chords are triads
starting on each of the different notes of the scale. Since
these chords are often expressed in terms of the root of
the chord, this fact is not always clear. Many tunes will
use just the three chords based on the fundamental (I), the
fourth (IV) and the fifth (V). Sometimes a fourth note
is added which is a third above the highest note of the
triad. This gives a 7th chord. When a minor third
is used it can result in the use of a note which is not
actually part of the original scale. For example,
the C major triad is CEG and a minor third above the
G is Bb, which is not part of the C major scale.
| Simple Triads for C Major scale | ||
|---|---|---|
| Notes of Chord | Name of Chord | Name Relative to Root* |
| CEG | C Major | I |
| DFA | d minor | ii |
| EGB | e minor | iii |
| FAC | F Major | IV |
| GBD | G Major | V |
| ACE | a minor | vi |
| BDF | b minor dim. | viio |
Some references:
J. Wild, "The computation behind consonance and dissonance,"
Interdisciplinary Science Reviews, Vol 27, No. 4, p 299 (2002).
H. Helmholtz, "On the sensation of tone as a physiological basis
for the theory of music," translated by A. J. Ellis, (Dover, NY, 1954).
Michael Keith, "From Polychords to Polya: Adventures in
Musical Combinatorics," Vinculum Press, Princeton, N.J., 1991,
ISBN 0-9630097-0-2.
Questions/Comments to: suits@mtu.edu
There are no pop-ups or ads of any kind on these pages. If you are seeing them, they are being added by a third party without the consent of the author.
Tto scales