Beats

When two (or more) sounds are present having a frequency difference of less than about 20 or 30 Hz, you will hear "beats." The frequency of the beats will be at the difference frequency. If the frequency difference is larger than about 20 or 30 Hz, a tone is usually perceived rather than distinct beats. For complex sounds, beats can arise from any of the partials of the sounds.

graph showing beats Mathematically beats can be understood from a mathematical identity for sine waves. For sounds with (angular) frequencies of w₁ and w₂ added together the identity gives
sin(w₁t) + sin(w₂t) = 2 sin(w₃t)cos( w₄t)
where w₃ is the average of w₁ and w₂ and w₄ is one half of their difference.

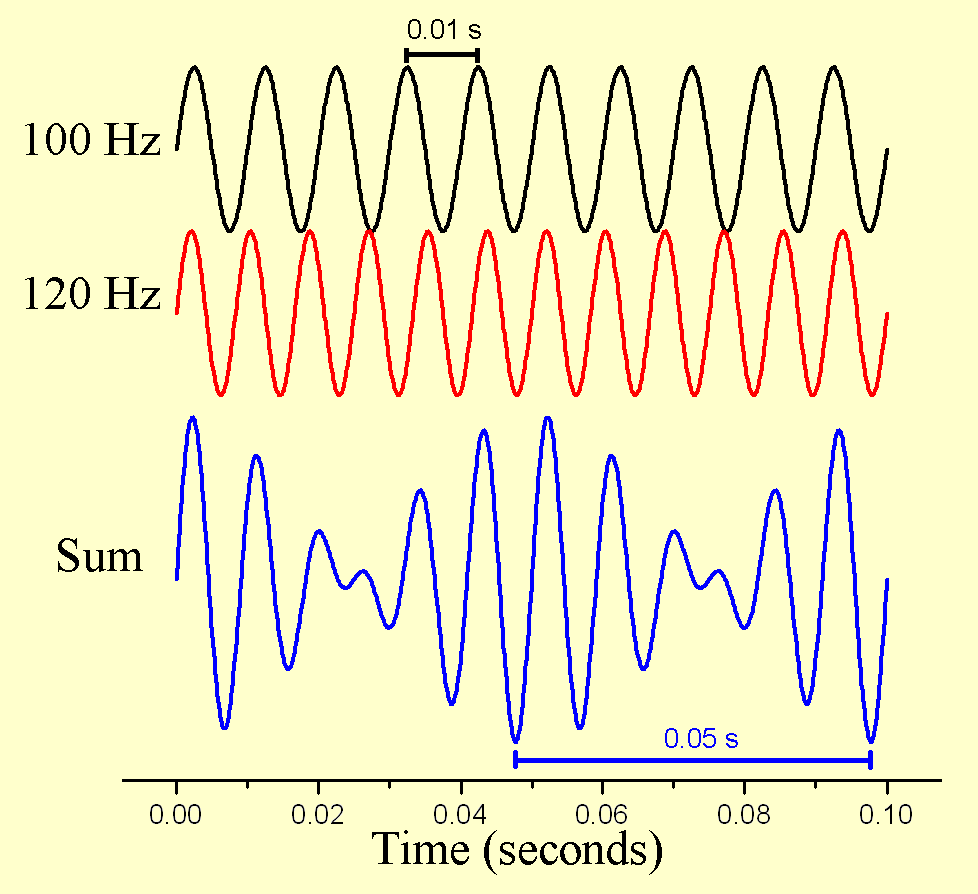
If the difference frequency is small, the sound is the sound of a single tone at the average frequency, but with a volume which varies in time at the difference frequency. This is illustrated on the graphic to the left. The sum is a sine wave with a variable amplitude and the pattern repeats every 0.05s. That is, there are 1/0.05 = 20 repeats per second.

You can hear beats using this Sound File (mp3) ( wav). There are two pure tones near middle C which are 6 Hz apart. First each tone is played separately using then left and right stereo channels, then they are played together. As an interesting experiment, listen to the sound file using a good pair of earphones. You will hear the beats even if the tones are sent separately to your two ears. This means your hearing system actually performs a (phase coherent) addition of the sounds somewhere in your brain, after the sound has been detected by your ear. The last sound in the file has the two tones played equally in both ears. The beats sound similar, but note also that it does not sound the same "spatially." See the wikipedia article on binaural beats for more information.

Beats can be used anytime you have periodic behavior. Since it is easy to hear beats faster than about 1 per second, it is relatively easy to match two signals with an accuracy of 1 Hz (or better) even if the original frequencies are microwave signals at 1 GHz = 1,000,000,000 or above. That corresponds to more than 12 digits of accuracy!

Questions/Comments to: suits@mtu.edu .

There are no pop-ups or ads of any kind on these pages. If you are seeing them, they are being added by a third party without the consent of the author.