Did you know you can compute square roots using a supply of resistors and an ohmmeter? Here's how.
If you have an infinite array of resistors
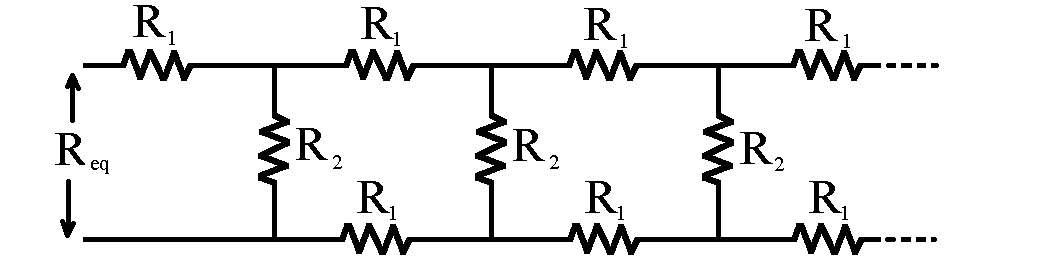
it is straightforward to show that the effective equivalent resistance, Req, of the
combination is given by the expression
.
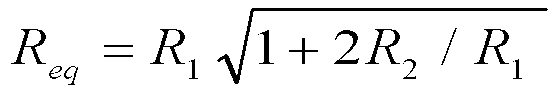Furthermore, by considering the array truncated after N units and computing Req
using the usual parallel and series combinations, you can show that as long as R1
and R2 are not too far different, the value converges to the inifinite case
to the precision of most resistors
even for a relatively small N. Here is a table of results obtained numerically.
| R2/R1 | N for 1% | N for 0.1% |
|---|---|---|
| 0.1 | 1 | 1 |
| 1 | 2 | 2 |
| 5 | 4 | 6 |
| 10 | 5 | 8 |
| 20 | 8 | 12 |
| 50 | 13 | 19 |
| 100 | 18 | 26 |
Hence, you can create an array with an equivalent resistance which is the square root of Y kiloohms, Y > 1, by choosing R1 = 1 kiloohm and R2 = (Y-1)/2 kiloohms using resistors of sufficient precision and enough sections to obtain the desired accuracy. In practice this will be very expensive for an accuracy greater than 0.1%. For values outside the range 1 < Y < 100, you can scale the value into that range by multiplying by powers of 100, and then adjust the answer using the same power, but of 10.
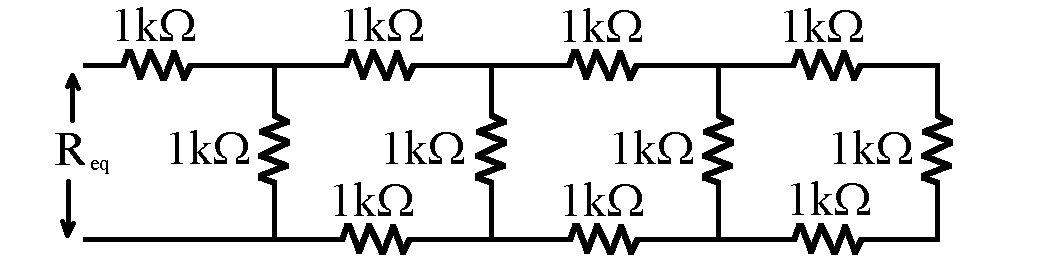
Example: This array uses N = 3 and has a resistance equal to the square root of 3 kiloohms
(to better than 0.1% if ideal resistors are used).
