| Moment: | Monopole | Dipole | Quadrupole |
|---|---|---|---|
| Example distribution: |
 |
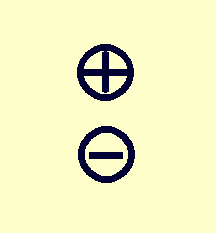 |
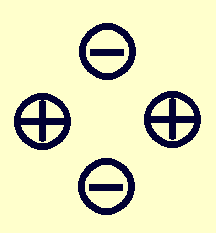 |
| Moment: | Monopole | Dipole | Quadrupole |
|---|---|---|---|
| Example distribution: |
 |
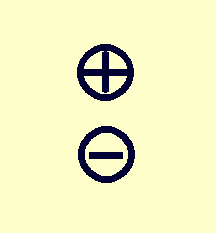 |
 |
When a nucleus is in its equilibrium position in a crystal, the net force on it is zero (by definition). Hence, the Monopole Electric moment (which is the charge of the nucleus, giving the force on it due to neighboring charges) will not lead to energy level splittings. On the other hand, deviations from spherical symmetry for both the nucleus and of the electric charges in the environment surrounding the nucleus can provide a torque on the nucleus and hence energy levels which depend on orientation. That is known as an electric quadrupole coupling.
Not all nuclei have an electric quadrupole moment. Due to symmetry considerations, for example, all nuclei which have a nuclear spin quantum number of 0 or 1/2 cannot have such a moment. Within the periodic table such spin quantum numbers are not all that common, but included are the common isotopes of Hydrogen, Oxygen, and Carbon. The most common isotope of Nitrogen, on the other hand, has a nuclear spin of 1 and a non-zero nuclear electric quadrupole moment.